Simulate Array Digital PCR

A function that simulates results of an array digital PCR.

sim_adpcr(m, n, times, n_panels = 1, dube = FALSE, pos_sums = FALSE)

Arguments

m

the total number of template molecules added to the plate. Must be a positive integer.

n

the number of chambers per plate. Must be a positive integer.

times

number of repetitions (see Details).

n_panels

the number of panels that are simulated by the function. Cannot have higher value than the times argument.

dube

if TRUE, the function is strict implementation of array digital PCR simulation (as in Dube et al., 2008). If FALSE, the function calculates only approximation of Dube's experiment. See Details and References.

pos_sums

if TRUE, function returns only the total number of positive (containing at least one molecule) chamber per panel. If FALSE, the functions returns a vector of length equal to the number of chambers. Each element of the vector represents the number of template molecules in a given chamber.

Value

If the pos_sums argument has value FALSE, the function returns a matrix with \(n\) rows and \(n_panels\) columns. Each column represents one plate. The type of such simulation would be "nm". If the pos_sums argument has value TRUE, the function returns a matrix with one row and \(n_panels\) columns. Each column contains the total number of positive chambers in each plate and type of simulation would be set as "tnp".

In each case the value is an object of the adpcr class.

Details

The array digital PCR is performed on plates containing many microfluidic chambers with a randomly distributed DNA template, fluorescence labels and standard PCR reagents. After the amplification reaction, performed independently in each chamber, the chambers with the fluorescence level below certain threshold are treated as negative. From differences between amplification curves of positive chambers it is possible to calculate both total number of template molecules and their approximate number in a single chamber.

The function contains two implementations of the array digital PCR simulation. First one was described in Dube at. al (2008). This method is based on random distributing \(m \times times\) molecules between \(n \times times\) chambers. After this step, the required number of plates is created by the random sampling of chambers without replacement. The above method is used, when the dube argument has value TRUE.

The second method treats the total number of template molecules as random variable with a normal distribution \(\mathcal{N}(n, 0.05n)\). The exact sum of total molecules per plate is calculated and randomly adjusted to the value of \(m \times times\). The above method is used, when the dube argument has value FALSE. This implementation is much faster than previous one, especially for big simulations. The higher the value of the argument times, the simulation result is closer to theoretical calculations.

References

Dube S, Qin J, Ramakrishnan R, Mathematical Analysis of Copy Number Variation in a DNA Sample Using Digital PCR on a Nanofluidic Device. PLoS ONE 3(8), 2008.

See also

sim_dpcr.

Examples

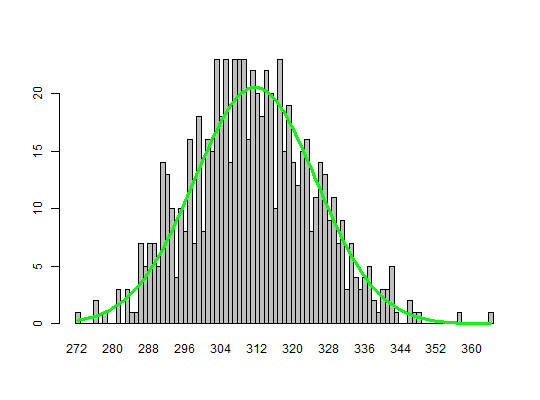
# Simulation of a digital PCR experiment with a chamber based technology.
# The parameter pos_sums was altered to change how the total number of positive 
# chamber per panel are returned. An alteration of the parameter has an impact 
# in the system performance.
adpcr_big <- sim_adpcr(m = 10, n = 40, times = 1000, pos_sums = FALSE, n_panels = 1000)
#> The assumed volume of partitions in each run is equal to 1.
#> The assumed volume uncertainty in each run is equal to 0.
adpcr_small <- sim_adpcr(m = 10, n = 40, times = 1000, pos_sums = TRUE, n_panels = 1000)
#> The assumed volume of partitions in each run is equal to 1.
#> The assumed volume uncertainty in each run is equal to 0.
# with pos_sums = TRUE, output allocates less memory
object.size(adpcr_big)
#> 536760 bytes
object.size(adpcr_small)
#> 171904 bytes

# Mini version of Dube et al. 2008 experiment, full requires replic <- 70000
# The number of replicates was reduced by a factor of 100 to lower the computation time.
replic <- 700
dube <- sim_adpcr(400, 765, times = replic, dube = TRUE,
    pos_sums = TRUE, n_panels = replic)
#> The assumed volume of partitions in each run is equal to 1.
#> The assumed volume uncertainty in each run is equal to 0.
mean(dube) # 311.5616
#> [1] 311.1357
sd(dube) # 13.64159
#> [1] 13.74987

# Create a barplot from the simulated data similar to Dube et al. 2008
bp <- barplot(table(factor(dube, levels = min(dube):max(dube))),
              space = 0)
lines(bp, dnorm(min(dube):max(dube), mean = 311.5, sd = 13.59)*replic,
      col = "green", lwd = 3)

# Exact Dube's method is a bit slower than other one, but more accurate
system.time(dub <- sim_adpcr(m = 400, n = 765, times = 500, n_panels = 500,
  pos_sums = TRUE))
#> The assumed volume of partitions in each run is equal to 1.
#> The assumed volume uncertainty in each run is equal to 0.
#>    user  system elapsed 
#>    0.47    0.00    0.50 
system.time(mul <- sim_adpcr(m = 400, n = 765, times = 500, n_panels = 500,
  pos_sums = FALSE))
#> The assumed volume of partitions in each run is equal to 1.
#> The assumed volume uncertainty in each run is equal to 0.
#>    user  system elapsed 
#>    0.58    0.01    0.59